Deep Learning – Reducción de dimensionalidad (PCA)

Exploraremos esta técnica y su uso en cuanto reducción de dimensionalidad. Buscaremos comprender su funcionamiento y utilidad en proyectos de inteligencia artificial

Usaremos MNIST para desarrollar este laboratorio. Descarga el dataset y realiza la normalización y aplanamiento de dimensiones

Entendamos PCA

PCA es una técnica lineal que permite la proyección de datos en un espacio de menor dimensión preservando la mayor cantidad posible de varianza original.

Para utilizarlo en nuestro proyecto debemos importarlo desde sklearn:

from sklearn.decomposition import PCA

Una vez implementado PCA definiremos la cantidad de componentes que deseamos trabajar. ¿Que indica la cantidad de componentes? Indica el número de componentes principales que se desean conservar después de realizar la reducción de dimensionalidad:

pca = PCA(n_components=2)
pca_train = pca.fit_transform(x_train)
pca_test = pca.transform(x_test)

¿Esto afecta la estructura de nuestro conjunto de datos?

Revisemos las variables pca_train y x_train

x_train tiene la siguiente estructura:

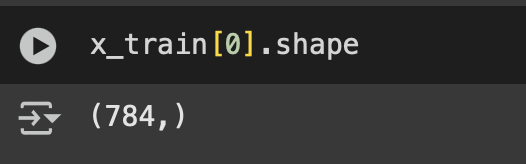
Mientras que pca_train tiene solo:

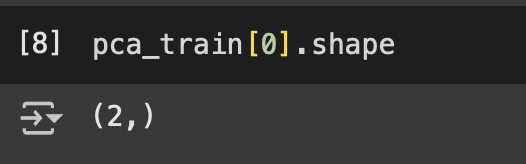
Reconstrucción

El método inverse_transform nos dará las imágenes reconstruidas a partir del aprendizaje de la transformación realizada con fit_transform:

x_train_reconstructed_pca = pca.inverse_transform(pca_train)
x_test_reconstructed_pca = pca.inverse_transform(pca_test)

Es decir un arreglo de 784

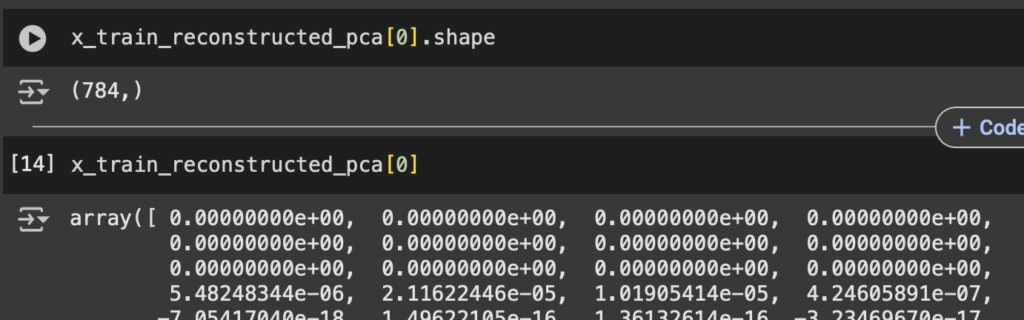
Métricas de error

¿Podemos tener números que muestren el error? Aplica MSE y podrás tener una métrica que sustente la interpretación de tus resultados

mse_train_pca = mean_squared_error(x_train, x_train_reconstructed_pca)
mse_test_pca = mean_squared_error(x_test, x_test_reconstructed_pca)

print(f"Error de reconstrucción en el entrenamiento con PCA: {mse_train_pca:.4f}")
print(f"Error de reconstrucción en la validación con PCA: {mse_test_pca:.4f}")

Nos da un número bastante bajo

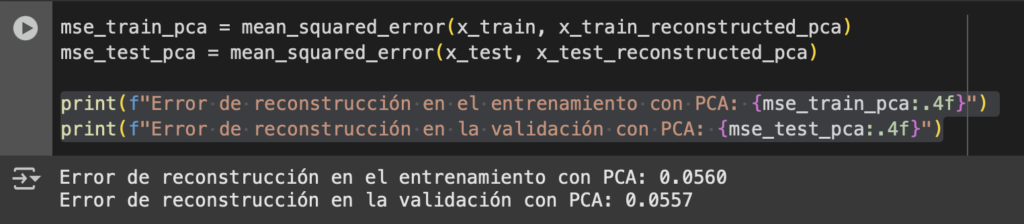
¿Quiere decir que vamos por buen camino? Validemos mostrando las reconstrucciones de nuestro conjunto de evaluación.

Decodifiquemos

Para facilitar la impresión de los resultados crearemos un método que nos permita reutilizarlo según el conjunto que utilicemos

def mostrar_imagenes(dataset, show=10):
  plt.figure(figsize=(20, 4))
  for i in range(show):
    ax = plt.subplot(2, show, i + 1)
    plt.imshow(dataset[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

Y podemos visualizar los datos de nuestro conjunto de datos antes y después de utilizar la técnica PCA

¿Qué pasó? ¿Por qué mi métrica me mostraba un número bajo y los números no se entienden? Recuerda como funciona MSE. Penaliza los errores grandes y tus datos están normalizados entre 0 y 1. La métrica que debemos utilizar es RMSE:

rmse_train_pca = root_mean_squared_error(x_train, x_train_reconstructed_pca)
rmse_test_pca = root_mean_squared_error(x_test, x_test_reconstructed_pca)

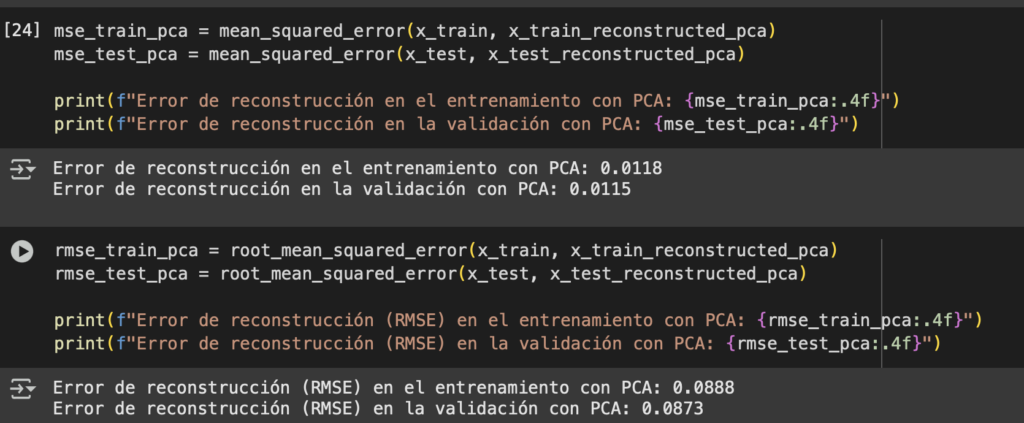
print(f"Error de reconstrucción (RMSE) en el entrenamiento con PCA: {rmse_train_pca:.4f}")
print(f"Error de reconstrucción (RMSE) en la validación con PCA: {rmse_test_pca:.4f}")

Ten en cuenta que esta métrica suavizará el error porque será un promedio, si quieres penalizar de una manera más severa puedes obtener una métrica de RMSE por cada imagen y calcular el promedio.

¿Cómo optimizamos el modelo?

Prueba subiendo el número de componentes hasta que obtengas un buen resultado, ¿Qué te parece si probamos ahora con 50?

Nuestras métricas disminuyeron notablemente. ¿Y como le fue a la reconstrucción de imágenes?

Ahora son más legibles

El número perfecto

¿Cómo podríamos determinar el número adecuado de componentes? Si no utilizas un valor de componentes PCA utilizará la mayor cantidad disponible con tu conjunto de datos. Podemos hacer lo siguiente:

pca_full = PCA().fit(x_train)
plt.plot(np.cumsum(pca_full.explained_variance_ratio_))
plt.xlabel('Número de componentes')
plt.ylabel('Varianza acumulada')
plt.grid(True)
plt.show()

Esto nos dará la relación entre la cantidad de componentes y la varianza

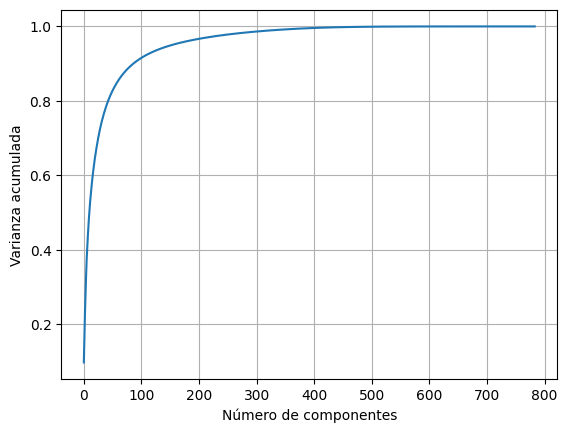
Podemos interpretar que un número de componentes cercano al 100 nos dará un buen resultado y que a partir de 200 componentes la ganancia no es significativa…

Conclusiones

• Las métricas de error deben aplicarse según la finalidad de los modelos, en este caso al aplicar MSE con data normalizada entre 0 y 1 podemos tener una falsa orientación de que el modelo está funcionando correctamente
• Para elegir el número ideal de componentes no es necesario ir con un número máximo, podemos considerar el uso de números óptimos. Esto es beneficioso cuando el conjunto de datos es extenso.
• Considera el uso de paradas anticipadas, así no exploras todas las combinaciones si no es necesario

Te recomiendo considerar el uso de métricas de error como: SSIM o PSNR. Para comparación de reconstrucciones visuales. 😉